12 models of multiplication

Posted on September 9, 2013 by MariaD — 9 Comments ↓ Tagged with: Lists, Multiplication

These models come from 24×36 inch full-color glossy poster.

–

–

Related Posts

• 6 ways to collect multiplication pictures
• 6 BIG adventures in #StreetMath
• Adaptations for toddlers and young kids

Like It? Share It.

• 
• 
• 
• 
• 
• 
• 
• 
• 
• 

‹ Adaptations for toddlers and young kids

6 ways to collect multiplication pictures ›

Posted in Grow

9 comments on “12 models of multiplication”

1. Shannon B. says:

   March 31, 2014 at 12:29 pm

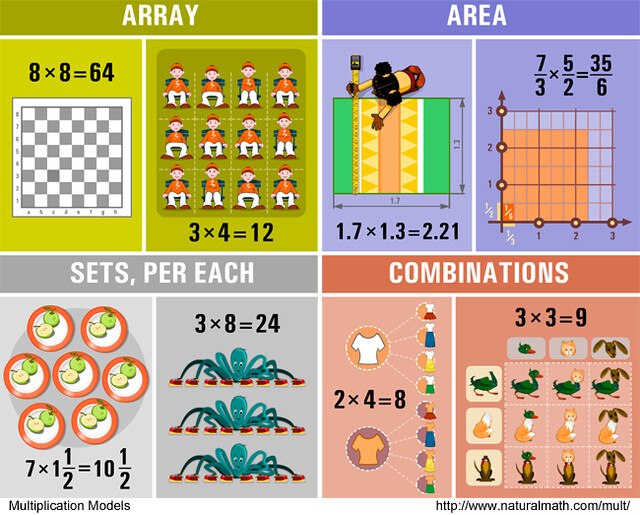
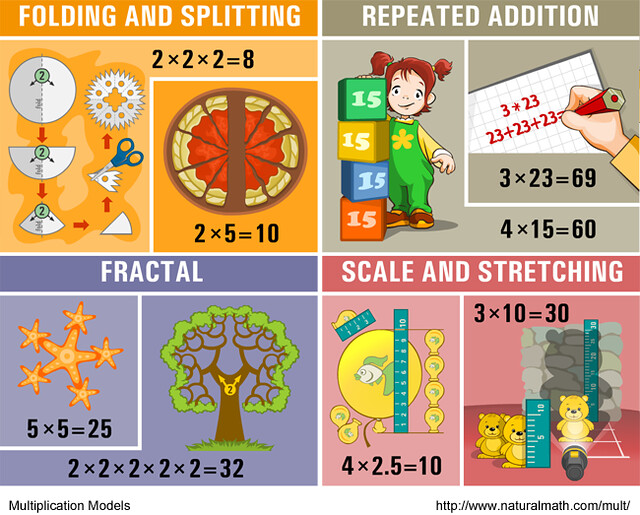
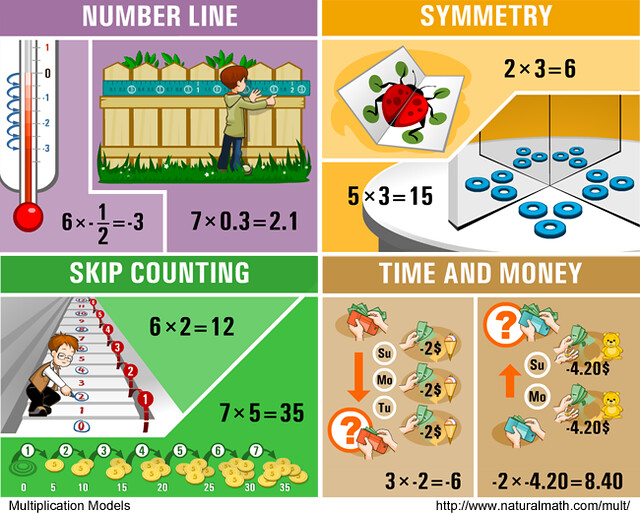
   I was wondering if I need to purchase or somehow print the 12 models of multiplication?
   Thank you

   Reply
   • MariaD says:

     March 31, 2014 at 12:49 pm

     Shannon, we will refer to the models in a few activities in the course. You are welcome to print these pictures, or look at them on the screen – this page will stay up! There is a big paper poster with the models for sale, as well. Whichever option makes more sense to you!

     Reply
     • Kristina says:

       February 2, 2015 at 3:43 am

       Is it possible to purchase an electronic version of the poster and then I could print one copy for myself? Shipping to Canada is $10. Thank you.

       Reply
       • MariaD says:

         February 2, 2015 at 7:51 am

         Kristina, we took the poster apart into the three sheets you see in the page above – http://www.moebiusnoodles.com/2013/09/12-models-of-multiplication/

         They fit on the regular printer paper. Here is a one-page version of the whole poster, if you want the whole thing for the reference https://farm3.staticflickr.com/2828/9712680940_7e56d54951_o.png

         Let me know if this helps, or if you need something else.

         The original paper poster is 18 by 24 inches, more than half as tall as I am!

         Reply
2. Joshua Greene says:

   November 2, 2015 at 4:21 am

   I’m delighted to say that I can add another model of multiplication to your list: prime factor concatenation.
   For example, 6 = 2 * 3 and 10 = 2 * 5, so 6* 10 = 2*2*3*5 = 60

   This was inspired by the game Prime Climb, so I really can’t take much credit for it. They use this to build a pretty multiplication table which illustrates the model nicely.

   Unfortunately, this makes 13 models of multiplication, which we know doesn’t allow us to create a nice array of models.

   Reply
   • MariaD says:

     November 2, 2015 at 7:09 am

     Joshua, thank you for your comment! I have good news and more good news :-)

     First, we do have plan to redesign the poster, something like “Even more models of multiplication” (since people suggested new ones since it came out). And the structure will be different – clustered by types of models and their relationships. I think it will come out first in our book on multiplication.

     Second, we need to separate “models and models” so to speak, and find good terms for them. What we have in that poster are bridges to the physical world: how objects (arrays, reflections, stretchy things) represent multiplication. What we need to have, separately, is how we can represent multiplication by other symbolic mathematics. Repeated addition will leave the original poster and go into that second collection. So will your concatenation.

     Do you know a good physical model of concatenation?

     Reply
3. Nitai Kshatriya says:

   May 27, 2016 at 7:25 am

   We are a team of volunteers and beginning a new plan in our group. Your web website provided us useful information to perform on. You’ve conducted a formidable process and our whole neighborhood might be thankful to you.|

   Reply
4. Joshua says:

   June 7, 2016 at 4:19 am

   This collection of models for multiplication remains one of my all-time favorite webpages for elementary school math. Taking a look again, I have the inkling of a pedagogical structure, so I am curious to hear other people’s thoughts:

   Models that can substitute for knowing multiplication facts: skip counting, repeated addition, array (maybe sets?). These are models where, if the student doesn’t know a multiplication fact, they can use the model to calculate a fact.

   Models that extend multiplication beyond positive integers: sets (one factor non-integer), number line (one factor non-integer), area (fractions and decimals, neither factor needs to be an integer, but both positive), scale (fractions and decimals, at least one positive factor), time and money (fractions, decimals, negatives).

   Models that connect multiplication to other math: combinations (combinations), fractals (exponentiation), symmetry (geometry), scaling (geometry), area (geometry), sets (division), splitting (fractions, division).

   Any thoughts?

   Reply
   • MariaD says:

     July 13, 2016 at 8:43 am

     Joshua, this is a good way to organize the poster. We are thinking of reprinting it, with a better organizational structure. Would you be interested in discussing it with me? If so, write reach.out@naturalmath.com and we can talk.

     Reply

2 Pings/Trackbacks for "12 models of multiplication"

1. How to Conquer the Times Table, Part 1 | DeniseGaskins.com says:

   January 27, 2016 at 8:48 pm

   […] see what multiplication looks like in real life, explore the multitude of Multiplication Models collected at the Natural Math website. Also available as a poster for easy […]

2. PUFM 1.5 Multiplication, Part 1 | DeniseGaskins.com says:

   February 8, 2016 at 1:44 am

   […] a model as fragile as “repeated addition.” Instead, explore the many real-life Multiplication Models collected at the Natural Math […]

This site uses Akismet to reduce spam. Learn how your comment data is processed.